百囚徒问题
这两天偶然刷到了一个油管博主讲解百囚徒问题,感觉非常有意思,思路非常好,所以决定记录下来。
本文内容来自Eugene Curtin,Max Warshauer. The locker puzzle,The Mathematical Intelligencer(2006):28-31
参考知乎 凉拌苦瓜 博主的文章:https://zhuanlan.zhihu.com/p/410614948
问题描述
在某个法制不健全的国家, 监狱中有编号1到100的100名死刑犯。监狱长给了他们最后一次机会:
一个房间里有100个抽屉,监狱长随意地把1到100这100个号码放入1号到100号抽屉中,每个抽屉一张。囚犯们逐个进入房间,每人可以任意打开50个抽屉,之后关上。如果每名囚犯都在这50个抽屉中发现了他的号码,那么所有的犯人都会被赦免;如果有人没有找到他的号码,那么所有的囚犯都会被处死。在第一个囚犯进入房间之前,囚犯们允许一起讨论开抽屉的“策略”,但一旦第一个囚犯进入房间,他们之间就被禁止交流。
寻找思路
如果纯粹随机开抽屉,那么所有人都被赦免的概率只有:
$(\frac{1}{2})^{100}\approx0.000000000000000000000000000000008$
这个概率相当于两个人在地球上找到同一粒沙子的概率,根本不可能
寻找线索,以原文为框架,尽量给出了一个正向寻找最佳策略的思路。但要注意最佳策略未必本来就是一个被正向找到的过程。
为了简化问题,我们先把囚徒成员数简化为10个,每个成员可以检查5个抽屉,这时随机策略的成功概率也只有$(\frac{1}{2})^{10}=(\frac{1}{1024})$了。
提高成功概率的一个思路是给每个人分配固定的5个抽屉去检查,我们可以先来验证一下这个猜测。假设我们制定的策略1为:1-5号成员检查1-5号抽屉,6-10号成员检查6-10号抽屉。那么他们成功的概率等于1-5号码牌刚好被分配到了1-5号抽屉中,概率为:
$(\frac{5}{10})(\frac{4}{9})(\frac{3}{8})(\frac{2}{7})(\frac{1}{6})=(\frac{1}{242})$
该策略成功的概率比随机策略提高了,但成功的概率仍然比较小。值得注意的是,prisoner1如果在该策略中找到了自己的号码,则prisoner6找到自己号码的概率为5/9,prisoner2找到自己号码的概率为4/9,即prisoner1是否成功与其他成员是否成功具有相关性。
那么我们猜想,在策略中提高不同成员检查结果的相关性可能会提高团队的成功概率。理想的策略是如果prisoner1成功,那么其他所有成员也会成功,这时团队成功的概率为1/2,当然很难实现(实际上无法实现),但我们可以找到一个使prisoner1与一部分成员成功的概率相同的策略,并验证在该策略下团队成功的概率。
完美策略方案 单向循环链表的运用
每个囚徒的策略,就是首先打开与自己编号相同的抽屉,从中取出号码牌,并打开号码牌所对应的抽屉。之后,重复此过程,直到找到自己的号码牌,或者50个抽屉的机会用完。 实际就是看抽屉是否存在大于51个元素的链表,如果都小于50,那么所有囚徒一定都可以存活。
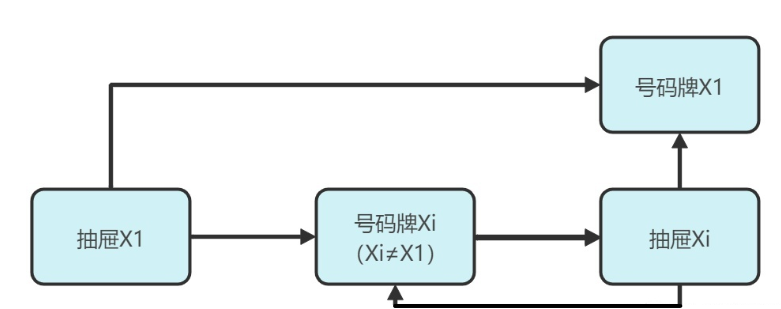
例如,29号囚徒首先打开了29号抽屉,里面放着51号的号码牌,于是他打开51号抽屉,里面放着18号的号码牌,于是他打开18号的抽屉,里面放着29号的号码牌,他完成了任务。
计算概率
比起计算“所有循环链表的长度不超过50”的概率,“有一个循环链表长度超过50”的概率更容易计算。因为“有一个循环链表的长度是51”和“有一个循环链表的长度是52”之类的事件是彼此互斥的(循环链表的长度总和是100,所以如果有大于50的链表,也只会存在一个),所以总概率就是它们的和。而对于$m>=51$,只需先选出$m$个元素,将它们构成一个环,之后再将剩下的元素随机打乱即可唯一地得到一种分布。
具体地说,所有形成长度为m环的映射种类为:
$C^m_{100}(m-1)!(100-m)!=100!/m$
全排列个数为$100!$
因此这个概率等于$P(m)=1/m$
综上,所有圆环长度不超过50的概率等于
$P=1-\sum_{m=51}^{100}\frac{1}{m}\approx0.312$
这个概率就是囚徒被释放的概率。当囚徒人数趋于无穷大时,概率趋向于:
$P=1-\sum_{m=N+1}^{2N}\frac{1}{m}\rightarrow1-ln2$
总结
不那么严密地说,这个策略的关键点在于让所有囚徒尽可能地一起成功或者一起失败,因此所有玩家的任务不再是独立的,一旦有一个人成功,他所翻出的号码牌对应的人也一定会成功,同时只要有一半的人成功,剩下的人都一定成功。
通过计算可得,在之前所有人都成功的条件下,下一个人成功的概率依次为
50%,75.25%,89.26%,95.63%,…
这个策略被证明最优。
一些感悟
我觉得这个问题精彩在于对于概率本质的理解,收获很多,也再一次感受到了数学的魅力。



